
2022
[News 07-09] Tutorial Scalable Design-Program-Compilation Optimizations for Quantum Algorithms at DAC
[News 07-30] The Quantum Neural Network Compression has been accepted by ICCAD [arXiv].
[News 09-21] Tutorial QuantumFlow+VACSEN at QuantumWeek
[News 10-10] Vitual Tutorial QuantumFlow+VACSEN at ESWEEK
2021
Resources @ University and Conference Talks
- Dec 05: ROAD4NN: Research Open Automatic Design for Neural Networks [Slides]
- Nov 11: VU ECE [Slides]
- Oct 30: IU ISE Colloquium [Slides]
Tutoiral Slides and Resources @ QuantumWeek and ESWEEK
[Session 1] [Session 2] [Session 3] [Session 4] [Session 5]
[News 01-21] The Quantum Machine Learning Course is Conducted at ND.
[News 12-20] The SS repo on implemening quantum neural networks using IBM Qiskit has released! Happy New Year!
[News 12-20] QuantumFlow has been accepted by Nature Communications.
[News 11-20] Invited to give a talk at ASP-DAC 2021 for a Special Session (SS) work.
[News 09-20] Invited to give a talk at IBM Quantum Summit to introduce QuantumFlow.
Framework: from Classical to Quantum
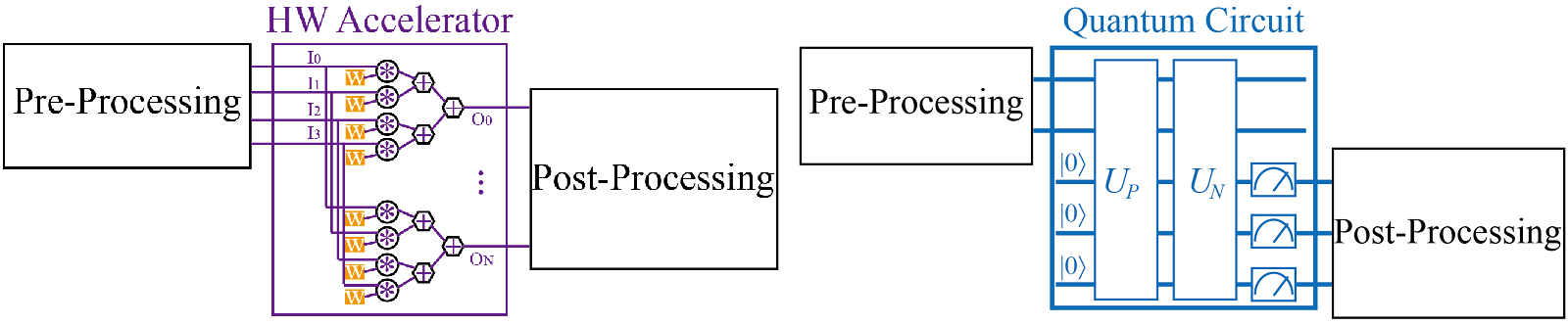
In the above figure, on the left-hand, it is the design framework for classical hardware (HW) accelerators. The whole procedure will take three steps: (1) pre-processing data, (2) accelerating the neural computations, (3) post-processing data.
Similarly, on the right-hand side, we can build up the workflow for quantum machine learning. It takes 5 steps to complete the whole computation: (1) PreP pre-processing data; (2) UP data encoding onto quantum, that is quantum-state preparation; (3) UN neural operation oracle on quantum computer; (4) M data readout, that is quantum measurement; (5) PostP post-processing data. Among these stpes, (1) and (5) are conducted on classical computer, and (2-4) are conducted on the quantum circuit.
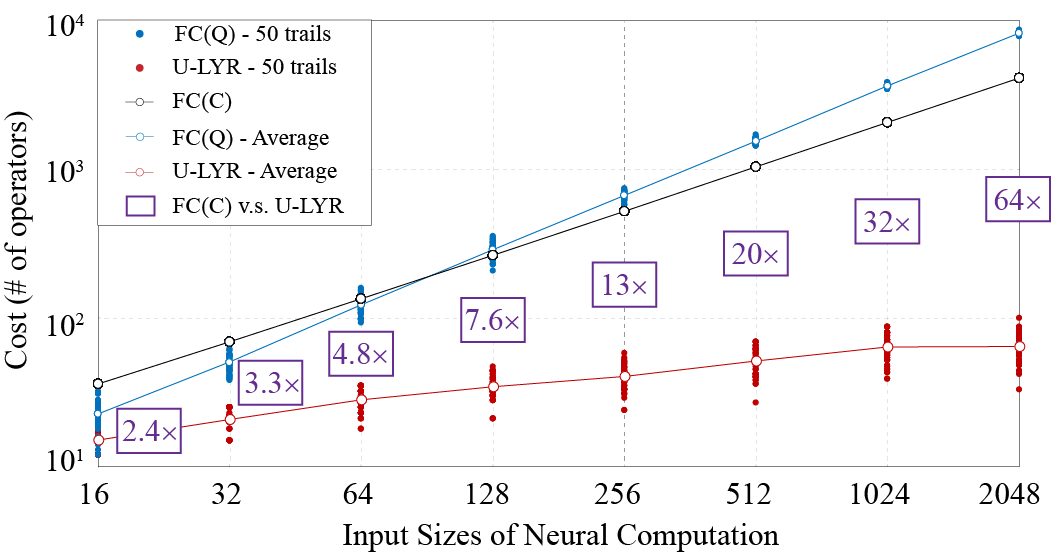
Quantum Advantage Achieved for Neural Computation
**When bridging the machine learning and quantum computing, the first and foremost question is why we need quantum computer for machine learning? We give the answer that the neural network computation on quantum computer can achieve quantum advantage. That is, for the cost complexity of O(2^N) on classical computer, a well-designed quantum implementation can reduce the cost to O(N^2).** The following figure reports the comparison results for the core component in neural network, the neural computation layer.
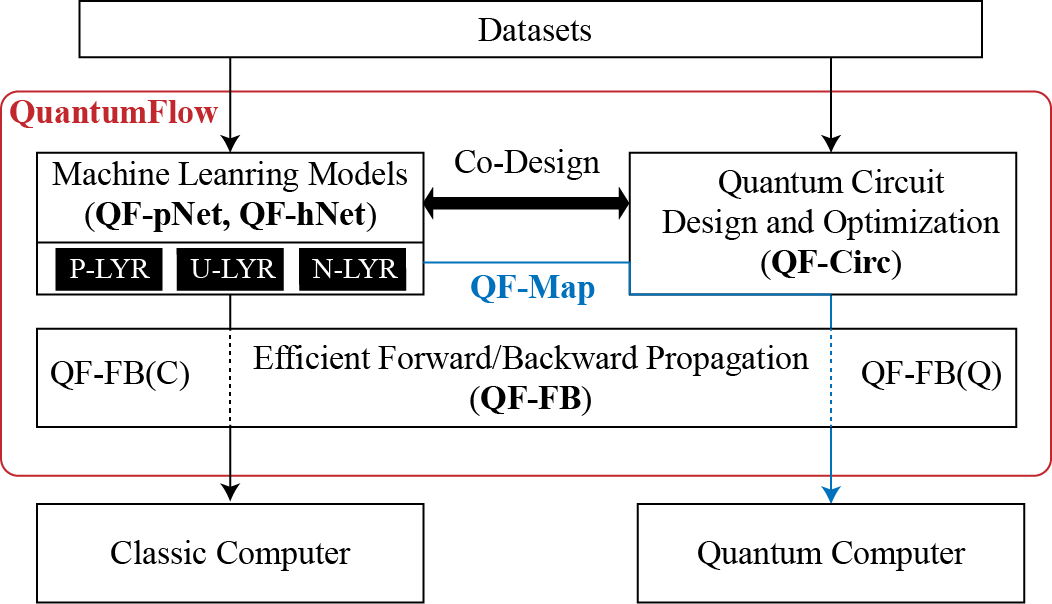
QuantumFlow Framework
The quantum advantage is achieved by co-design the neural network and quantum circuit. In the paper, we propose the first co-design framework, namely QuantumFlow, to design quantum-friendly neural network and optimize quantum circuit leveraging the network's property to reduce the cost complexity from O(2^N) to O(N^2). We demonstrate QuantumFlow in the following figure, and please refer to our [NCOMMS paper](https://www.nature.com/articles/s41467-020-20729-5) for detailed info.
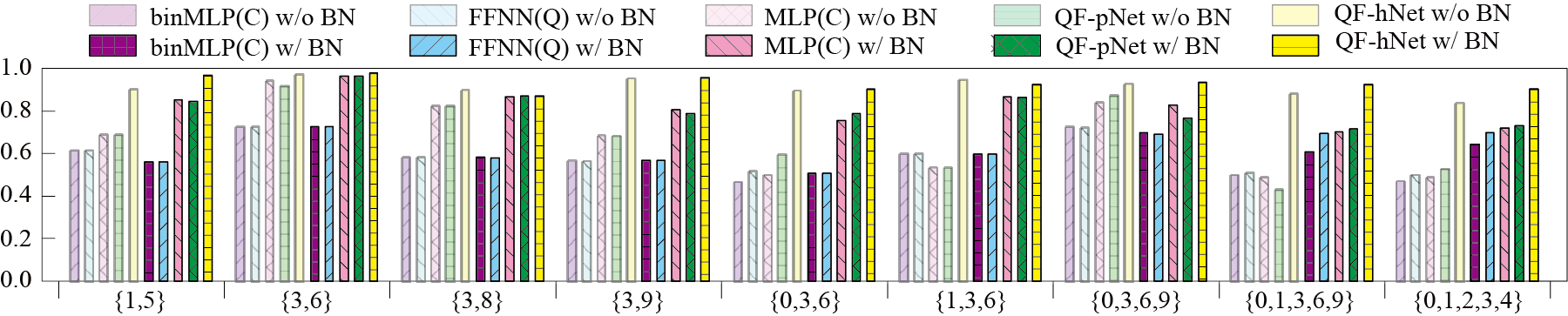
QF-Nets on MNIST
The quantum-friendly QF-Nets achieves over 90% accuracy on different subsets from MNIST. In our [Demo](/2020/08/04/blog_2020-08-04-QFDemo1/), we demonstrate how to map QF-Nets for {3,6} sub-dataset from MNIST onto quantum circuits on quirk with 16 qbits, whose accuracy is 95.73%.
Related work on This Special Session
The work accepted by Nature Communications.
@article{jiang2020co,
title={A Co-Design Framework of Neural Networks and Quantum Circuits Towards Quantum Advantage},
author={Jiang, Weiwen and Xiong, Jinjun and Shi, Yiyu},
journal={arXiv preprint arXiv:2006.14815},
year={2020}
}
The work invited by ASP-DAC 2021.
@article{jiang2020machine,
title={When Machine Learning Meets Quantum Computers: A Case Study},
author={Jiang, Weiwen and Xiong, Jinjun and Shi, Yiyu},
journal={arXiv preprint arXiv:2012.10360},
year={2020}
}
Contact
Weiwen Jiang
Email: wjiang2@nd.edu
Web: https://wjiang.nd.edu/

